جذع (رياضيات)

  لمعانٍ أخرى، طالع جذع (توضيح).

جذع (رياضيات) معلومات عامة زمرة التناظر Cnv, [1,n], (*nn)

في الهندسة، جِذْع أو مجسم ناقص أو المنقوص (باللاتينية: frustum) هو جزء من مجسم (عادة هرم أو مخروط) يقطعه مستوى واحد أو مستويين متوازيين. قاعدته الأساسية مضلعة، وأوجهه الجانبية شبه منحرفة. الجذع القائم (right frustum) أو الهرم الناقص هو هرم منتظم أو مخروط منتظم مقطوع عموديًا على محوره.

إذا كانت كل حواف الجذع لها نفس الطول (شكل متساوي الأضلاع)، فهو منشور منتظم .

جذع المشاهدة في الرسومات الحاسوبية، هو هرم مقطوع يمثل منطقة ثلاثية الأبعاد على الشاشة. طريقة استبعاد الجذع "frustum culling" من طرق تحديد السطح المخفي .

الجذع في صناعة الطيران، يكون على شكل مخروط مقطوع ويستخدم كغطاء للحمولة بين مرحلتين فيصاروخ متعدد المراحل (مثل ساتورن 5).

جذع

العناصر والحالات الخاصة والمفاهيم المتعلقة بها

جذع مربع

يمكن إنشاء "جذع مثلث" باستخدام ثماني السطوح

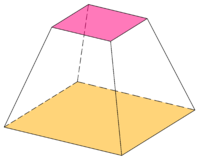
محور الجذع هو محور المخروط أو الهرم الأصلي. يكون الجذغ دائريًا إذا كانت قاعدته دائرية؛ ومنتظم إذا كان المحور عموديًا على كلتا القاعدتين، ومائل بخلاف ذلك.

ارتفاع الجذع هو المسافة العمودية بين مستوىات القاعدتين.

يمكن اعتبار المخروط والهرم حالات خاصة للجذع، حيث يمر أحد المستويات القاطعة عبر القمة (حيث تُمَثَّلْ القاعدة هنا بنقطة تقاطع المستوى مع نقطة رأس الهرم أو المخروط)، الجذع الهرمي هي فئة فرعية من المنشورات.

جذعان اثنان بقاعدتين متطابقتين متصلتين يصنعان جذع ثنائي .

الصيغ الرياضية

الحجم

قدمت الرياضيات المصرية القديمة معادلة حجم الجذع الهرمي في بردية موسكو الرياضية، المكتوبة في الأسرة الثالثة عشر (ق. 1850 BC):

$V=\frac{h}{3}(a^2+ab+b^2),$

حيث a هو طول ضلع القاعدة وb هو طول ضلع السطح، وh هو الارتفاع.

عرف المصريون الصيغة الصحيحة لحجم مثل هذا الهرم المربع المبتور، لكنها ظهرت بغير برهان في بردية موسكو.

حجم الجذع المخروطي أو الهرمي هو حجم الجسم قبل قطع «القمة»، مطروحًا منه حجم «القمة» المقطوعة هذه:

$V=\frac{h_1{B}_1-h_2{B}_2}{3},$

حيث B₁ وB₂ هما مساحتي القاعدة والسطح، وh₁ وh₂ هما الارتفاعات العمودية من القمة لمستويات القاعدة والسطح.

مع الأخذ في الاعتبار أن

$\frac{B_1}{h_1^2}=\frac{B_2}{h_2^2}=\frac{\sqrt{B_1{B}_2}}{h_1{h}_2}=\alpha ,$

يمكن التعبير عن صيغة الحجم على أنها ثلث جداء النسبة $\alpha$ مع فرق مكعبات الارتفاعات h₁ وh₂ فقط:

$V=\frac{h_1\alpha h_1^2-h_2\alpha h_2^2}{3}=\alpha \frac{h_1^3-h_2^3}{3}.$

باستخدام المتطابقة a³ − b³ = (a − b)(a² + ab + b²) ، يحصل المرء على:

$V=(h_1-h_2)\alpha \frac{h_1^2+h_1{h}_2+h_2^2}{3},$

حيث h₁ − h₂ = h هو ارتفاع الجذع.

بتوزيع $\alpha$ والتعويض من تعريفها، نحصل على المتوسط الهيروني للمساحات B₁ وB₂ :

$\frac{B_1+\sqrt{B_1{B}_2}+B_2}{3};$

لذا فإن الصيغة البديلة هي:

$V=\frac{h}{3}(B_1+\sqrt{B_1{B}_2}+B_2).$

اشتهر هيرو السكندري باشتقاقه لهذه الصيغة ومعها واجه الوحدة التخيلية: الجذر التربيعي لسالب واحد.

للتحديد:

• حجم المخروط الدائري هو:

$V=\frac{\pi h}{3}(r_1^2+r_1{r}_2+r_2^2),$

حيث r₁ وr₂ هما نصف قطر القاعدة والسطح.

• حجم الجذع الهرمي الذي تكون قواعده عبارة عن n -مضلع منتظم (حيث n تمثل عدد الضلوع) هو:

$V=\frac{nh}{12}(a_1^2+a_1{a}_2+a_2^2)\cot \frac{\pi }{n},$

حيث a₁ وa₂ هما طولا ضلعي القاعدة والسطح.

frustum الهرمي

مساحة السطح

جذع مخروطي

نموذج ثلاثي الأبعاد لمجسم ناقص مخروطي الشكل.

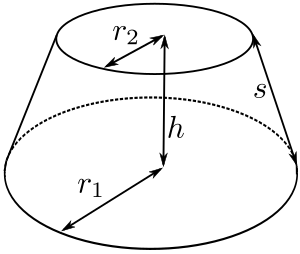
للجذع المخروطي الدائرية المنتظم

$\begin{array}{rr}\text{Lateral surface area}& =\pi (r_1+r_2)s\\ & =\pi (r_1+r_2)\sqrt{{(r_1-r_2)}^2+h^2}\end{array}$

و

$\begin{array}{rr}\text{Total surface area}& =\pi ((r_1+r_2)s+r_1^2+r_2^2)\\ & =\pi ((r_1+r_2)\sqrt{{(r_1-r_2)}^2+h^2}+r_1^2+r_2^2)\end{array}$

حيث r ₁ وr ₂ هما نصف قطر القاعدة والسطح على الترتيب، وs هو الارتفاع المائل للجذع.

مساحة سطح الجذع المنتظم الذي له قواعد من مضلعات عادية متشابهة وعدد جوانبها n هي

$A=\frac{n}{4}[(a_1^2+a_2^2)\cot \frac{\pi }{n}+\sqrt{{(a_1^2-a_2^2)}^2{\sec }^2\frac{\pi }{n}+4h^2{(a_1+a_2)}^2}]$

حيث a1 وa2 هما جانبي القاعدتين.

أمثلة

شوكولاتة ماركة رولو لها تقريبا شكل جذع مخروطي دائري منتظم، على الرغم من أنها ليست مسطحة في الأعلى.

• على ظهر ورقة الدولار النقدية الأمريكية، يظهر جذع هرمي مقابل لختم الولايات المتحدة العظيم، تعلوه عين العناية الإلهية.
• مركز جون هانكوك في شيكاغو، إلينوي هو عبارة عن جذع وقواعده مستطيلة.
• نصب واشنطن هو جذع هرمي ضيق مربع الشكل يعلوه هرم صغير.
• في الترجمة الإنجليزية لمجموعة القصص القصيرة لسنانيسواف ليم The Cyberiad، تدعي قصيدة الحب وجبر الموترات أن «كل جذع يتوق إلى أن يكون مخروطًا».
• الدلاء وأغطية المصابيح النموذجية هي أمثلة يومية على الجذوع المخروطية.

روابط خارجية

• اشتقاق صيغة لحجم جذع هرمي ومخروط (Mathalino.com)
• إيريك ويستاين، Pyramidal frustum، ماثوورلد Mathworld (باللغة الإنكليزية).

• إيريك ويستاين، Conical frustum، ماثوورلد Mathworld (باللغة الإنكليزية).