نظام متغير الكتلة

الصواريخ التي تفقد جزأ من كتلتها كالوقود أثناء الطيران.

النظام متغير الكتلة في الميكانيكا هو المادة التي تتغير كتلتها بمرور الزمن. إنه من الخطأ محاولة تطبيق قانون نيوتن الثاني للحركة على مثل هذه الأنظمة. يمكن حساب الكتلة والتي تعتمد على الزمن عن طريق إعادة ترتيب قانون نيوتن الثاني بإضافة جزأ على المعادلة يقوم بحساب زخم الحركة المتسبب بواسطة الكتلة التي تخرج أو تدخل للنظام. 

${\mathbf{F}}_{\mathrm{e}\mathrm{x}\mathrm{t}}+{\mathbf{v}}_{\mathrm{r}\mathrm{e}\mathrm{l}}\frac{\mathrm{d}m}{\mathrm{d}t}=m\frac{\mathrm{d}\mathbf{v}}{\mathrm{d}t}$

حيث:

F_{ext هي محصلة القوى الخارجية على الجسم.}

vrel هي السرعة النسبية للكتلة الداخلة أو الخارجة بالنسبة لمركز ثقل الجسم. 

v هي سرعة الجسم.

في الميكانيكا المدراية التي تتعامل مع ميكانيكا الصواريخ، فإن vrel يشير إلى سرعة الخروج الفعلية ويرمز لها ve.

استنتاج

هناك استنتاجات عديدة لمعادلة الحركة للأنظمة متغيرة الكتلة والتي تعتمد على ما إذا كانت الكتلة داخلة أو خارجة للنظام ( هل تزداد كتلة الجسم أو تقل؟). ولتبسيط الحسابات يمكن افتراض أن جميع الأجسام عبارة عن جسيمات. نفرض أيضا أن هذه الكتلة لا ينتج عنها قوة خارجية تؤثر على الجسم.

ازدياد الكتلة

عند اللحظة الأولى كلتة dm  لها سرعة نسبية u على وشك الالتحام مع الجسم الذي كلتله m وله سرعة v. اللحظة 2 كلا الجسمين يتحركان بسرعة v+dv بعد زمن dt.

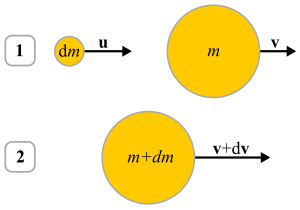
الاستنتاج القادم هو لنظام تزداد كتلته. نفرض ان هناك جسم له كتلة متغيرة m تتحرك بسرعة v عند زمن ابتدائي t. عند هذه اللحظة نفرض ان هناك جسيم كتلته dm يتحرك بسرعة u. كمية الحركة الابتدائية يمكن التعبير عنها بالصورة التاليه:

${\mathbf{p}}_{\mathrm{1}}=m\mathbf{v}+\mathbf{u}\mathrm{d}m$

والآن عند زمن يساوى t+dt، نفرض ان الجسم الرئيسي والجسيم الملتحم به يتحركون بسرعة v+dv. لذلك معادلة كمية الحركة الجديدة ستكون:

${\mathbf{p}}_{\mathrm{2}}=(m+\mathrm{d}m)(\mathbf{v}+\mathrm{d}\mathbf{v})=m\mathbf{v}+m\mathrm{d}\mathbf{v}+\mathbf{v}\mathrm{d}m+\mathrm{d}m\mathrm{d}\mathbf{v}$

بما أن dmdv هو حاصل ضرب قيمتين صغيرتين، فيمكننا إهماله. لذلك خلال فترة زمنية dt فإن كمية الحركة للنظام تكون:

$\mathrm{d}\mathbf{p}={\mathbf{p}}_{\mathrm{2}}-{\mathbf{p}}_{\mathrm{1}}=(m\mathbf{v}+m\mathrm{d}\mathbf{v}+\mathbf{v}\mathrm{d}m)-(m\mathbf{v}+\mathbf{u}\mathrm{d}m)=m\mathrm{d}\mathbf{v}-(\mathbf{u}-\mathbf{v})\mathrm{d}m$

ومن ثم، من قانون نيوتن الثاني:

${\mathbf{F}}_{\mathrm{e}\mathrm{x}\mathrm{t}}=\frac{\mathrm{d}\mathbf{p}}{\mathrm{d}t}=\frac{m\mathrm{d}\mathbf{v}-(\mathbf{u}-\mathbf{v})\mathrm{d}m}{\mathrm{d}t}=m\frac{\mathrm{d}\mathbf{v}}{\mathrm{d}t}-(\mathbf{u}-\mathbf{v})\frac{\mathrm{d}m}{\mathrm{d}t}$

لاحظ ان u-v هي سرعة dm بالنسبة إلى m ويمكن التعبير عنها بـ vrel. يمكن كتابة المعادلة كالآتي:

${\mathbf{F}}_{\mathrm{e}\mathrm{x}\mathrm{t}}+{\mathbf{v}}_{\mathrm{r}\mathrm{e}\mathrm{l}}\frac{\mathrm{d}m}{\mathrm{d}t}=m\frac{\mathrm{d}\mathbf{v}}{\mathrm{d}t}$

إزالة الكتلة أو طردها

في الأنظمة التي تخرج من الكتلة أو يتم إزالتها فإن الإستنتاج يكون مختلف قليلا. عند زمن t، نفرض ان هناك كتلة m تتحرك بسرعة v ولذلك فإن كمية الحركة الابتدائية للنظام تكون:

${\mathbf{p}}_{\mathrm{1}}=m\mathbf{v}$

وبما أن النظام يفقد كتلة مقدارها dm فإنها تكون سالبة بمعنى أنه بعد زمن t+dt تكون كمية الحركة:

${\mathbf{p}}_{\mathrm{2}}=(m+\mathrm{d}m)(\mathbf{v}+\mathrm{d}\mathbf{v})+\mathbf{u}(-\mathrm{d}m)=m\mathbf{v}+m\mathrm{d}\mathbf{v}+\mathbf{v}\mathrm{d}m+\mathrm{d}m\mathrm{d}\mathbf{v}-\mathbf{u}\mathrm{d}m$

حيث u هي سرعة الكتلة المطرودة. لذلك كمية الحركة ستكون:

$\mathrm{d}\mathbf{p}={\mathbf{p}}_{\mathrm{2}}-{\mathbf{p}}_{\mathrm{1}}=(m\mathbf{v}+m\mathrm{d}\mathbf{v}+\mathbf{v}\mathrm{d}m-\mathbf{u}\mathrm{d}m)-(m\mathbf{v})=m\mathrm{d}\mathbf{v}-(\mathbf{u}-\mathbf{v})\mathrm{d}m$

وهذه هي نفس معادلة dp في حالة إضافة كتلة.

نماذج

عند انطلاقه فإن بالون الصاروخ يطلق جزأ من كتلته كالهواء مما يسبب تسارع كبير.

من تعريف العجلة a = dv/dt لذلك معادلة الحركة للأنظمة متغيرة الكتلة يمكن كتابتها:

${\mathbf{F}}_{\mathrm{e}\mathrm{x}\mathrm{t}}+{\mathbf{v}}_{\mathrm{r}\mathrm{e}\mathrm{l}}\frac{\mathrm{d}m}{\mathrm{d}t}=m\mathbf{a}$

في الأجسام التي لا يمكن معاملتها على أنها جسيمات، يجب أن نغير a بـ acm وتعني تسارع مركز ثقل الجسم:

${\mathbf{F}}_{\mathrm{e}\mathrm{x}\mathrm{t}}+{\mathbf{v}}_{\mathrm{r}\mathrm{e}\mathrm{l}}\frac{\mathrm{d}m}{\mathrm{d}t}=m{\mathbf{a}}_{\mathrm{c}\mathrm{m}}$

لذلك فإن القوة الناتجة عن الدفع تعرف بـ:

${\mathbf{F}}_{\mathrm{t}\mathrm{h}\mathrm{r}\mathrm{u}\mathrm{s}\mathrm{t}}={\mathbf{v}}_{\mathrm{r}\mathrm{e}\mathrm{l}}\frac{\mathrm{d}m}{\mathrm{d}t}$  وبذلك:

${\mathbf{F}}_{\mathrm{e}\mathrm{x}\mathrm{t}}+{\mathbf{F}}_{\mathrm{t}\mathrm{h}\mathrm{r}\mathrm{u}\mathrm{s}\mathrm{t}}=m{\mathbf{a}}_{\mathrm{c}\mathrm{m}}$

هذه المعادلة تبين أن الجسم يمكن أن يكون له تسارع نتيجة الدفع حتى لو لم تؤثر عليه قوة خارجية. لو أن محصلة القوى Fnet تساوى مجموع Fext و Fthrust لذلك فإن المعادلة تكون:

${\mathbf{F}}_{\mathrm{n}\mathrm{e}\mathrm{t}}=m{\mathbf{a}}_{\mathrm{c}\mathrm{m}}$

معادلة الصاروخ المثالي

معدلات كتلة صاروخ مقابل السرعة النهائية محسوبة من معادلة الصاروخ

يمكن استخدام معادلة الصاروخ المثالي للمركبات التي لها نفس سلوكه (تحرك نفسها ع طريق تخليها عن جزأ من كتلتها، مادة دافعة وبسرعة عالية). يمكن اشتقاقها من معادلة الحركة للأنظمة متغيرة السرعة كما يلي: عندما لا تؤثر قوة خارجية (Fext = 0) على الجسم فإن معادلة الحركة تكون:

${\mathbf{v}}_{\mathrm{r}\mathrm{e}\mathrm{l}}\frac{\mathrm{d}m}{\mathrm{d}t}=m\frac{\mathrm{d}\mathbf{v}}{\mathrm{d}t}$

إذا كانت سرعة المادة الدافعة vrel تتحرك في اتجاه عكسي لحركة الصاروخ dv/dt فإن الكمية القياسية لهذه المعادلة تكون:

$-v_{\mathrm{r}\mathrm{e}\mathrm{l}}\frac{\mathrm{d}m}{\mathrm{d}t}=m\frac{\mathrm{d}v}{\mathrm{d}t}$

$-v_{\mathrm{r}\mathrm{e}\mathrm{l}}\mathrm{d}m=m\mathrm{d}v$

يتم التكامل عن طريق فصل المتغيرات:

$-v_{\mathrm{r}\mathrm{e}\mathrm{l}}\underset{m_0}{\overset{m_1}{\int }}\frac{\mathrm{d}m}{m}=\underset{v_0}{\overset{v_1}{\int }}\mathrm{d}v$

$v_{\mathrm{r}\mathrm{e}\mathrm{l}}\ln \frac{m_0}{m_1}=v_1-v_0$

بإعادة ترتيب المعادلة  Δv = v1 - v0  فإننا نصل للمعادلة النهائية للصاروخ:

$\mathrm{\Delta }v=v_{\mathrm{r}\mathrm{e}\mathrm{l}}\ln \frac{m_0}{m_1}$

حيث: 

m0 هي الكتلة الابتدائية الكلية وتشمل المادة الدافعة.

m1 هي الكتلة الكلية النهائية.

vrel هي سرعة الخروج الفعالة.

Δv هو التغير الأقصى لسرعة المركبة عندما لا تؤثر قوة خارجية عليها.