|
تضامنًا مع حق الشعب الفلسطيني |
مكعب فيرما
اذهب إلى التنقل
اذهب إلى البحث
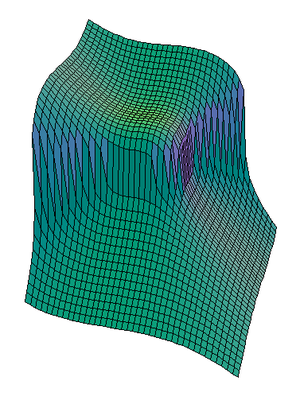
في علم الهندسة، مكعب فيرما سُمي من قبل بيير دي فيرما، وهو عبارة عن سطح معرّف بالعلاقة:
وباستخدام الهندسة الجبرية نحصل على العلاقات الوسيطية لمكعب فيرما بالشكل الآتي:
وفي الفضاء5 الإسقاطي تُعطى المعادلة بالشكل:
يمكن بسهولة وصف السبع وعشرون خط الموجودين على مكعب فيرما وفق الآتي: يوجد 9 خطوط تُعطى بالشكل (w : aw : y : by)، حيث a و b أرقام ثابتة مكعبها -1، لها 18 مرافق وذلك حسب الإحداثيات المُستخدمة.[1][2]
مراجع
- ^ "معلومات عن مكعب فيرما على موقع mathworld.wolfram.com". mathworld.wolfram.com. مؤرشف من الأصل في 2020-07-20.
- ^ "معلومات عن مكعب فيرما على موقع d-nb.info". d-nb.info. مؤرشف من الأصل في 2020-10-31.