دورة (فيزياء)

  لمعانٍ أخرى، طالع دورة (توضيح).

البندول: دورة تكرر نفسها.

الدورة في الفيزياء (بالإنجليزية: Period) أو الزمن الدوري هو الزمن اللازم لعمل دورة كاملة، أو اهتزازة كاملة ويقاس بوحدة الثانية (في النظام الدولي أو العالمي SI)، وتطبق على الدوال الزمنية مثل هزاز توافقي ودوال تعتمد على الزمن والمكان في حساب الموجات. وبالنسبة للدورة المعتمدة على الزمن والمكان يفرق بين:

• زمن الدورة: بالنسبة لعملية تتكرر بطريقة منتظمة بعد فترة زمنية ثابتة،
• طول دورة: بالنسبة لتكرار عملية معينة بعد مسافة معينة (مثال على ذلك الحركة الانتقالية على شبكة بلورية أو شبكة الصياد).

وفي تلك المقالة سنتعامل مع الدالة المعتمدة على الزمن وحده.

أقرب مثال على دورة معتمدة على الزمن دورة الأرض حول الشمس تعيد نفسها كل 365 وربع يوم.

وصفها الرياضي

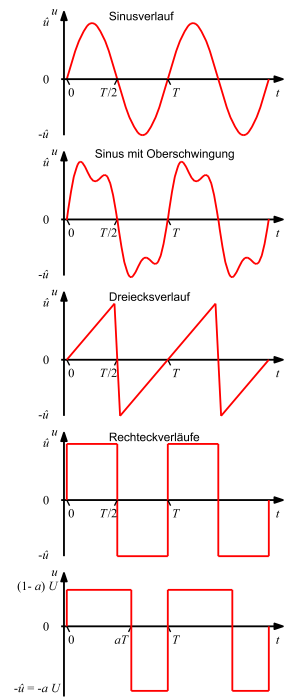
تسمى الدورة أيضا زمن الدورة ويرمز لها بالحرف T. ومثال آخر لدالة دورية نجدها في التيار المتردد كما في الشكل. كما يصحب التيار المتردد تردد الفلولطية.

تغير دوري : المحور الأفقي يبين الزمن ، والمحور الرأسي يبين متغير فيزيائي ، مثل شدة التيار أو الجهد الكهربائي مثلا. أقصى قيمة لـ y تسمى مطال (بالإنجليزية: amplitude).

أمثلة لجهد كهربائي يتغير دوريا: فوق جهد متردد، (2) جهدين مختلفين متطابقين، (3) تغير الجهد في شكل سن المنشار (يستخدم في التلفزة، (4)و (5) مثالين لتغير جهد مربع الشكل.

وتمثل الدورة رياضيا بالمعادلة:

$f(t)=f(t+T)$

وهي تنطبق لكل نقطة زمنية t حيث الدورة T = ثابت > 0

$f=\frac{1}{T}.$

وفي المعاملة الرياضية للهندسة الكهربائية يستعان كثيرا ب تردد زاوي ω لتسهيل الحسابات، حيث:

$\omega =2\pi f=\frac{2\pi }{T}.$

ومثال على ذلك: يستخدم تيار متردد في البيوت ذو تردد 50 هرتز، ولذلك فله زمن دورة مقداره:

$T_{50}=\frac{1}{50\mathrm{H}\mathrm{z}}=1/50\mathrm{s}=20\mathrm{m}\mathrm{s}$

حيث m s ملي ثانية.

وعند تمثيل عمليات دوال جيبية يستبدل الزمن t أحيانا بالزاوية φ = ωt كمتغير في الدالة. عندئذ يصبح زمن الدورة هو بالتمام دورة كاملة عبر 360 درجة، أي:

ωT = 2π

= 360°

= 2π راديان

القياس

يقاس زمن الدورة في الغالب بواسطة دورات إلكترونية تقوم بالعد مثل عدادات الكهرباء، كما يمكن قياس الزمن الدوري لبندول بسيط يتحرك حركة توافقية بسيطة بالعلاقة التالية:

$T=2\pi \sqrt{\frac{L}{g}}$

'L': طول خيط البندول

'g': عجلة الجاذبية

كما يمكن قياس الزمن الدوري لنابض مرن (زنبرك) يتحرك حركة توافقية بسيطة بالعلاقة التالية:

$T=2\pi \sqrt{\frac{M}{K}}$

'M': كتلة الثقل المعلق بالنابض

'K': ثابت المرونة للنابض (ثابت هوك)

الموجات

تتغير الموجات كدالة للزمن والمكان. فمثلا موجة صوتية أو موجة كهرومغناطيسية نفرق بين:

• زمن الدورة عند حدوث تغير دوري يعاد كل فترة زمنية ثابتة،
• طول الدورة عند حدوث التغير بعد مسافات ثابتة.

(مثال على «الدورة المكانية» نجده في تتابع أعمدة النور في شارع، فهي دورية وعلى مسافات متساوية.)

يمكن وصف امثال تلك الدوال الموجية رياضيا بدالة جيبية تنتشر على المحور x وهو يمثل المكان. فيكون متغير الدالة الجيبية هو المكان.

الصيغة العامة لتغير قيمة فيزيائية كدالة للزمن وللمكان في نفس الوقت هي:

$\phi =2\pi (\frac{t}{T}\pm \frac{x}{\lambda })+{\phi }_0$

حيث:

λ طول الموجة ، ومقلوبها

1/λ يسمى العدد الموجي.

بالنسبة إلى موجة تنتشر في الاتجاه x نطبق الإشارة السالبة.

دورة مدارية

المقالة الرئيسية: دور مداري

يدور القمر حول الأرض. ويمكن اختيار عدة نقاط مرجعية يكتمل عندها دورة كاملة 360° : بقياس دورة القمر مع اعتبار حركة الأرض حول الشمس أو بعدم أخذ حركة الأرض في الاعتبار.

رقاص

المقالة الرئيسية: رقاص

ساعات "سيجموند ريفلر" الدقيقة .

رقاص الساعة يتحرك من نهاية عظمى يمنى إلى نهاية عظمى يسرى. يستغرق رقاص الساعة بين النهاية العظمى اليمنى إلى النهاية العظمى اليسرى والعودة إلى النهاية العظمى اليمنى 1 ثانية. فيكون زمن دورته 1 ثانية. يعتمد زمن الدورة على طول القضيب الخفيف الحامل. فإذا كانت الساعة تؤخر وجب تقصير طول الرقاص (بإزاحة الثقل قليلا إلى أعلى على القضيب الخفيف الحامل)، وإذا كانت الساعة تقدم وجب زيادة طول الرقاص (إزاحة الثقل إلى أسفل على القضيب الخفيف الحامل).

اقرأ أيضا

• طول الموجة
• طور موجة
• حساب التيار المتردد
• نباض
• صوت