تكامل إهليلجي

في الحساب التكاملي، نشأت التكاملات الإهليلجية أو التكاملات الناقصية (بالإنجليزية: Elliptic integral)‏ في الأصل فيما يتعلق بمشكلة إيجاد طول القوس للقطع الناقص. تم دراستها لأول مرة من قبل جوليو فاغنانو وليونهارت أويلر (حوالي 1750). تعرف الرياضيات الحديثة «التكامل الإهليلجي» على أنه أي دالة f يمكن التعبير عنها على شكل:

$f(x)=\underset{c}{\overset{x}{\int }}R(t,\sqrt{P(t)})\mathrm{d}t,$

حيث R هي دالة كسرية ذات متغيرين، و P هي متعددة الحدود من الدرجة الثالثة أو الرابعة بدون جذور متكررة، و c هو ثابت.

بشكل عام، لا يمكن التعبير عن التكاملات في هذا الشكل بدلالة الدوال الابتدائية. الاستثناءات لهذه القاعدة العامة هي عندما يكون لـ P جذور متكررة، أو عندما لا تحتوي R (x, y) على قوى فردية لـ y.

تدوين العمدة

التكاملات الاهليلجية غير التامة هي دوال لعمدتين (arguments). أما التكاملات الاهليلجية التامة، فهي دوال لعمدة واحدة.

• α: الاختلاف المركزي الزاوي
• k = sin α: الاختلاف المركزي.
• m = k² = sin² α: الوسيط

التكاملات الإهليلجية غير التامة

التكامل الإهليلجي غير التام من النوع الأول

يعرف التكامل الإهليلجي غير الكامل من النوع الأول F بـ:

$F(\phi ,k)=F(\phi |k^2)=F(\sin \phi ;k)=\underset{0}{\overset{\phi }{\int }}\frac{\mathrm{d}\theta }{\sqrt{1-k^2{\sin }^2\theta }}.$

هذا هو الشكل المثلثي للتكامل؛ بتعويض t = sin (θ) و x = sin (φ)، نحصل على شكل ليجاندر الإهليلجي النظامي:

$F(x;k)=\underset{0}{\overset{x}{\int }}\frac{\mathrm{d}t}{\sqrt{(1-t^2)\cdot (1-k^2{t}^2)}}.$

بدلالة السعة φ والاختلاف المركزي الزاوي:

$F(\phi \setminus \alpha )=F(\phi ,\sin \alpha )=\underset{0}{\overset{\phi }{\int }}\frac{\mathrm{d}\theta }{\sqrt{1-(\sin \theta \sin \alpha {)}^2}}.$

في هذا الترميز، يشير استخدام شريط عمودي كمحدد إلى أن العمدة (argument) التي تليها هي «الوسيط»، بينما تشير الشرطة المائلة للخلف إلى أنها «الاختلاف المركزي الزاوي». يشير استخدام الفاصلة المنقوطة إلى أن العمدة التي تسبقها هي جيب السعة.

التكامل الإهليلجي غير التام من النوع الثاني

تكتب التكاملات الإهليلجية من النوع الثاني على الشكل المثلثي:

$E(\phi ,k)=E(\phi |k^2)=E(\sin \phi ;k)=\underset{0}{\overset{\phi }{\int }}\sqrt{1-k^2{\sin }^2\theta }\mathrm{d}\theta .$

شكل جاكوبي:

$E(x;k)=\underset{0}{\overset{x}{\int }}\frac{\sqrt{1-k^2{t}^2}}{\sqrt{1-t^2}}\mathrm{d}t.$

وبالمثل، مع الاختلاف المركزي الزاوي:

$E(\phi \setminus \alpha )=E(\phi ,\sin \alpha )=\underset{0}{\overset{\phi }{\int }}\sqrt{1-(\sin \theta \sin \alpha {)}^2}\mathrm{d}\theta .$

يعطى طول قوس الزوال من خط الإستواء إلى دائرة العرض بـ E:

$m(\phi )=a(E(\phi ,e)+\frac{{\mathrm{d}}^2}{\mathrm{d}{\phi }^2}E(\phi ,e)),$

حيث a هو المحور الرئيسي للإهليلج (القطع الناقص)، و e هو إختلافه المركزي.

التكامل الإهليلجي غير التام من النوع الثالث

تكتب التكاملات الإهليلجية غير التامة من النوع الثالث Π على الشكل المثلثي:

$\mathrm{\Pi }(n;\phi \setminus \alpha )=\underset{0}{\overset{\phi }{\int }}\frac{1}{1-n{\sin }^2\theta }\cdot \frac{\mathrm{d}\theta }{\sqrt{1-(\sin \theta \sin \alpha {)}^2}}$

أو

$\mathrm{\Pi }(n;\phi |m)=\underset{0}{\overset{\sin \phi }{\int }}\frac{1}{1-n{t}^2}\cdot \frac{\mathrm{d}t}{\sqrt{(1-m{t}^2)(1-t^2)}}.$

يُطلق على العدد n اسم المميزة ويمكن أن يأخذ أي قيمة، بغض النظر عن العمدات الأخرى. ومع ذلك، لاحظ أن $\mathrm{\Pi }(1;\frac{\pi }{2}|m)$ لانهائي، مهما كان m.

يعطى طول قوس الزوال من خط الإستواء إلى دائرة العرض φ أيضا بدلالة Π:

$m(\phi )=a(1-e^2)\mathrm{\Pi }(e^2;\phi |e^2).$

التكاملات الإهليلجية التامة

هي حالات خاصة للتكاملات غير التامة عندما تكون السعة تساوي π/2، وبالتالي x=1.

التكامل الإهليلجي التام من النوع الأول

منحنى التكامل الإهليلجي التام من النوع الأول K(k)

تعرف التكاملات الإهليلجية التامة من النوع الأول K بـ:

$K(k)=F(\frac{\pi }{2},k)=F(\frac{\pi }{2}|k^2)=F(1;k)=\underset{0}{\overset{\pi /2}{\int }}\frac{\mathrm{d}\theta }{\sqrt{1-k^2{\sin }^2\theta }}=\underset{0}{\overset{1}{\int }}\frac{\mathrm{d}t}{\sqrt{(1-t^2)(1-k^2{t}^2)}},$

يمكن استخدام مفكوكه:

$K(k)=\frac{\pi }{2}\sum _{n=0}^{\mathrm{\infty }}{[\frac{(2n)!}{2^{2n}(n!{)}^2}]}^2{k}^{2n}$

يمكن حسابه بكفاءة عالية بدلالة المتوسط الحسابي الهندسي:

$K(k)=\frac{\frac{\pi }{2}}{\mathrm{a}\mathrm{g}\mathrm{m}(1,\sqrt{1-k^2})}.$

التكامل الإهليلجي التام من النوع الثاني

منحنى التكامل الإهليلجي التام من النوع الثاني $E(k)$

تعرف التكاملات الإهليلجية التامة من النوع الثاني E بـ:

$E(k)=E(\frac{\pi }{2},k)=E(1;k)=\underset{0}{\overset{\pi /2}{\int }}\sqrt{1-k^2{\sin }^2\theta }\mathrm{d}\theta =\underset{0}{\overset{1}{\int }}\frac{\sqrt{1-k^2{t}^2}}{\sqrt{1-t^2}}\mathrm{d}t$.

بالنسبة للقطع الناقص ذو المحور الرئيسي a والمحور الثانوي b، وبالتالي من الاختلاف المركزي $e=\sqrt{1-b^2/a^2}$، التكامل الإهليلجي التام من النوع الثاني E (e) يساوي ربع المحيط c للقطع الناقص قسمة المحور الثانوي a. اختصارًا:

$c=4aE(e)$

يمكن استخدام مفكوكه:

$E(k)=\frac{\pi }{2}\sum _{n=0}^{\mathrm{\infty }}{[\frac{(2n)!}{2^{2n}(n!{)}^2}]}^2\frac{k^{2n}}{1-2n}=\frac{\pi }{2}\{1-{(\frac{1}{2})}^2\frac{k^2}{1}-{(\frac{1\cdot 3}{2\cdot 4})}^2\frac{k^4}{3}-\cdots -{[\frac{(2n-1)!!}{(2n)!!}]}^2\frac{k^{2n}}{2n-1}-\cdots \}.$

حيث $n!!$ هو عاملي ثنائي.

التكامل الإهليلجي التام من النوع الثالث

منحنى التكامل الإهليلجي التام من النوع الثالث $\mathrm{\Pi }(n,k)$ مع عدة قيم ثابتة لـ n $n$

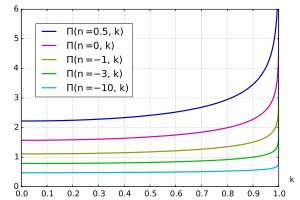
تعرف التكاملات الإهليلجية التامة من النوع الثالث Π بـ:

$\mathrm{\Pi }(n,k)=\underset{0}{\overset{\pi /2}{\int }}\frac{\mathrm{d}\theta }{(1-n{\sin }^2\theta )\sqrt{1-k^2{\sin }^2\theta }}.$

يمكن تعريفهم أحيانًا بالمعكوس الجمعي للمميزة n،

${\mathrm{\Pi }}^{\prime }(n,k)=\underset{0}{\overset{\pi /2}{\int }}\frac{\mathrm{d}\theta }{(1+n{\sin }^2\theta )\sqrt{1-k^2{\sin }^2\theta }}.$

انظر أيضًا

• منحنى إهليلجي