|
تضامنًا مع حق الشعب الفلسطيني |
قوس جيب التمام
| دالة قوس جيب التمام | |
|---|---|
التمثيل البياني للدالة
| |
| تدوين | |
| دالة عكسية | على المجال |
| مشتق الدالة | |
| مشتق عكسي (تكامل) |
|
| الميزات الأساسية | |
| مجال الدالة | |
| المجال المقابل | |
| قيم محددة | |
| القيمة/النهاية عند الصفر | |
| الحدود الأعلى | -1 |
| الحدود الأدنى | 1 |
| القيمة/النهاية عند 1 | 0 |
| القيمة/النهاية عند -1 | π |
| جذور الدالة | 1 |
| نقاط ثابتة | 0.7390851332152... |
| تعديل مصدري - تعديل | |
في الرياضيات، دالة قوس جيب التمام[1][2] (بالإنجليزية: Arccosine) لعدد حقيقي المحصور بين –1 و 1 هي الدالة العكسية لدالة جيب التمام، مستقرها هو ، وحدتها هي الراديان.
الدالة التي ترفق بكل عدد حقيقي المحصور بين –1 و 1 قيمة قوس جيب التمام الخاص به يرمز لها بـ arccos أو cos -1. ومن ثم تكون الدالة العكسية لدالة جيب التمام المثلثية المقتصرة إلى المجال .
في المَعْلم الديكارتي المتعامد والمتجانس (متعامد ممنظم) للمستوي، يتم الحصول على التمثيل البياني لدالة قوس جيب تمام الزاوية انطلاقا من التمثيل البياني لدالة جيب التمام المقتصرة إلى المجال بواسطة انعكاس حول المحور ذو المعادلة y = x.
مشتق
دالة جيب التمام العكسية تقبل الإشتقاق على المجال ]–1, 1[ ودالتها المشتقة هي:
إثبات
يمكن كتابة مشتقة الدالة بهذه الصيغة:
نضع :
إثبات آخر
يمكن إيجاد مشتقة دالة arccos(x) عن طريق تفاضل مركب دالتين (دالة ومعكوسها):
- إذا كانت cos(arccos(x)) = x بتفاضل الطرفين معاً ينتج:
أي أن:
يُستنتج من ذلك:
بترتيبها تنتج المشتقة:
الشكل التكاملي
يمكن كتابة هذه الدالة على شكل التكامل المحدد:
المشتق العكسي
يمكن الحصول على المشتق العكسي لدالة قوس الجيب عن طريق التكامل بالتجزئة:
العلاقة بين قوس الجيب وقوس جيب التمام
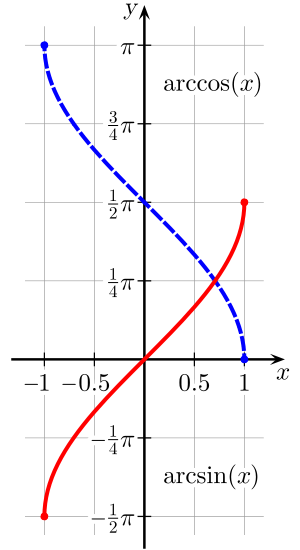
لكل عدد حقيقي x محصور بين –1 و 1 :
إثبات
يمكن أن نستنتج العلاقة بين arccos(x) و arcsin(x) كالتالي:
نأخذ:
يعني:
ومنه:
أي:
و بترتيبها نحصل على:
إثبات آخر
نشتق الدالة :
- وهي مساوية للصفر ، إذن arccos(x) + arcsin(x) هي عبارة عن دالة ثابتة.
نستنتج من ذلك أن:
مجموع arccos(x) و arcsin(x) عدد حقيقي ثابت (لأن مشتقة الثابت هي الصفر) يتم تعيينه أي أن:
نأخذ arcsin(x) إلى الطرف الآخر:
ندخل دالة الجيب تمام على الطرفين:
نبسط التعبير باستعمال قاعدة جيب تمام فرق عددين:
أي أن:
و بتعويض x ب 0 و التبسيط نحصل على:
بادخال دالة معكوس جيب التمام على الطرفين نحصل على:
أي أن:
و بالتالي نحصل على العلاقة بينهما:
التمثيل بواسطة متسلسلة
لدينا:
و بتعويض arcsin(x) بمتسلسلتها نحصل على متسلسلة دالة arccos(x) :
على المستوي العقدي
الشكل اللوغاريتمي

يمكن التعبير عن دالة قوس جيب التمام باستخدام اللوغاريتم العقدي:
طالع أيضًا
مراجع
- ^ ميشال إبراهيم ورامي أبو سليمان وفادي (1 يناير 2007). قاموس المصطلحات العلمية - انكليزي/فرنسي/عربي. دار الكتب العلمية. ISBN:978-2-7451-5445-3. مؤرشف من الأصل في 2020-03-19.
{{استشهاد بكتاب}}: يحتوي الاستشهاد على وسيط غير معروف وفارغ:|بواسطة=(مساعدة) - ^ مجمع اللغة العربية بالقاهرة (1957). مجموعة المصطلحات العلمية والفنية التي أقرها المجمع. مؤرشف من الأصل في 2020-08-28.
{{استشهاد بكتاب}}: يحتوي الاستشهاد على وسيط غير معروف وفارغ:|بواسطة=(مساعدة)
| قوس جيب التمام في المشاريع الشقيقة: | |

