قطب (تحليل مركب)

  لمعانٍ أخرى، طالع قطب (توضيح).

القيمة المطلقة لدالة غاما. هذا الشكل يشير إلى أن الدوال تؤول إلى ما لا نهاية له عند الأقطاب (اليسار). في اليمين، دالة غاما ليس لها أقطاب بل تتصاعد بوتيرة كبيرة.

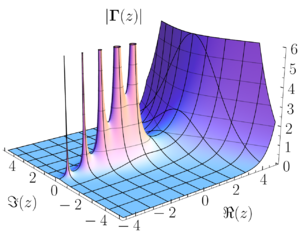
في التحليل المركب، قطب (بالإنجليزية: Pole)‏ دالة جزئية الشكل هو نوع ما من خصوصية تتصرف كما تتصرف خصوصية الدالة $\frac{1}{z^n}$ عندما يكون z مساويا للصفر. إذا كان a قطبا لدالة ما (f(z، فإن هذه الدالة تؤول إلى ما لا نهاية له عندما يقترب z من a.

تعريف

ليكن U مجموعة مفتوحة من المستوي المركب C وليكن a عنصرا من U ولتكن f دالة f : U \ {a} → C، حيث f دالة تامة الشكل على نطاقها. إذا وجدت دالة g تامة الشكل g : U → C حيث (g(a مختلف عن الصفر، ووجد عدد صحيح موجب n حيث يتوفر ما يلي مهما كان z في {U \ {a:

$f(z)=\frac{g(z)}{(z-a{)}^n}$

فإن a يسمى قطبا للدالة f.

$f(z)=\frac{1}{h(z)}$

$f(z)=\frac{a_{-n}}{(z-a{)}^n}+\cdots +\frac{a_{-1}}{(z-a)}+{\sum }_{k\ge 0}{a}_k(z-a{)}^k.$

أمثلة

• الدالة

$f(z)=\frac{3}{z}$

لها قطب من الدرجة الأولى 1 (قطب بسيط) عند $z=0$.

• الدالة

$f(z)=\frac{z+2}{(z-5{)}^2(z+7{)}^3}$

لها قطب من الدرجة الثانية عند $z=5$ وقطب من الدرجة الثالثة عند $z=-7$.

• الدالة

$f(z)=\frac{z-4}{e^z-1}$

لها أقطاب من الدرجة الأولى 1 عند $z=2\pi ni\text{ for }n=\dots ,-1,0,1,\dots .$ من أجل مشاهدة ذلك، اكتب $e^z$ على شكل متسلسلة تايلور حول أصل المعلم.

• الدالة

$f(z)=z$

له قطب وحيد عند ما لا نهاية له، وهو من الدرجة الأولى.

انظر أيضا

• جذر دالة (تحليل مركب)
• نظرية التحكم
• راسب (تحليل مركب)