|
تضامنًا مع حق الشعب الفلسطيني |
موجة جيبية

المَوْجة الجَيْبِيّة (بالإنجليزية: Sine wave) هي منحنى رياضياتي يصف تذبذبًا دوريًا أملسًا.[1] الموجة الجيبية هي موجة مستمرة؛ سمّيت نسبةً لمنحنى دالة الجيب. كثيراً ما تظهر في الرياضيات، الفيزياء وكذلك في الهندسة الكهربائية.
تصف هذه الدالة أو بالأحرى منحنى الدالة انتشار الصوت، وانتشار الموجات الكهرومغناطيسية مثل الضوء، وانتقال التيار الكهربائي المتردد، بالإضافة إلى معالجة الإشارات الصوتية والكثير من المجالات الأخرى. واسمها يرجع إلى أنها تعتمد على حساب الجيب أو جيب التمام.
أبسط صورة للدالة هي:
وهي تصف دالة متعلقة بالزمن (t). الدالة «دورية» بمعنى أنها تعيد نفسها، فمثلا يزداد التيار الكهربائي (باعتبار تيار متردد) رويدا رويدا حتى يصل إلى قمة ثم ينخفض رويدا رويدا حتى يعود إلى الصفر ويستمر في الانخفاض (أسفل المحور السيني) حتى يصل إلى القاع، ثم يزداد التيار رويدا رويدا حتى يصل إلى الصفر ثانيا. بذلك تكون الدورة قد اكتملت ويتميز وقتها «بزمن الدورة». يُسمى التيار عند القمة بالمطال، والمطال عند القمة يساوي المطال عند القاع، ولكنه معكوس الاتجاه (أي مختلف الإشارة).
في المعادلة السابقة:
- A هي قيمة المطال، أي أعلى قيمة تصل إليها الدالة - Amplitude.
- هي التردد الزاوي (بوحدات راديان/ثانية.)
- هي الطور أو الإزاحة الزاوية phase (يمكن في المسائل البسيطة إهمال الطور، وذلك من خلال اعتبار قيمته صفرية)
- t تشير إلى الزمن.
في الرسم أعلاه نجد منحنيين واحد منهما هو دالة لـ (sin (x والأخرى لـ (cos (x، ونلاحظ أنه عندما تكون (sin (x عند أقصاها (أي عند المطال) تكون الدالة (cos (x قد وصلت إلى الصفر. وهذا الحال يتكرر في الموجة، فكلما مضي «زمن دورة» تعود الدالتان وتأخذ كل منهما قيمتها عند بدء الدورة. إذا اعتبرنا الدالتين في الرسم تمثلان موجتان واقعيتان (مثل موجتي ماء في البحر أو تغير تيارين كهربائيين مترددين في سلك) فيمكن القول بأن الموجتين «منزاحتي الطور» بمقدار عن بعضهما البعض.
تمثيلها
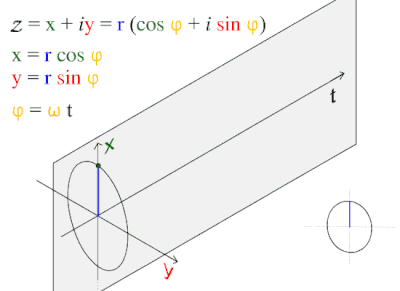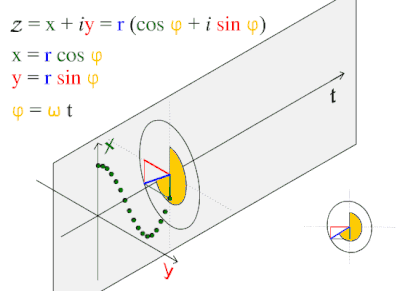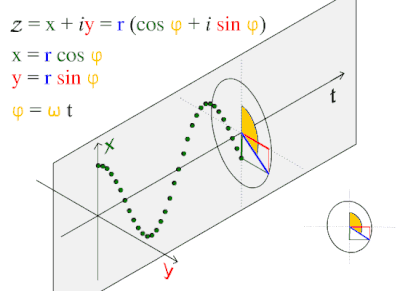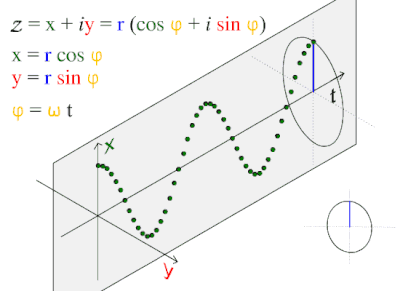
تتشكل الموجات كثيرا في الظواهر الطبيعية مثل موجات البحر، وموجات الصوت والموجات الضوئية. وهي تمثل أيضا اختلاف الليل والنهار. وتغير درجة الحرارة عبر اليوم أو السنة فكلها ظواهر دورية، ويمكن تمثيلها بدالة جيبية بسيطة.
وعند رسم جهد تيار متردد نجد أنه يشبه موجة جيبية. بحيث يُمكن حساب الموجة كموجة جيبية أو كموجة جيب التمام حيث أن:
هي الأخرى موجة جيبية ذات طور منحاز بمقدار .
وتستطيع الأذن البشرية التعرف على الموجة الجيبية في صورة الصوت حيث أن الموجة الجيبية ما هي إلا تمثيل لتردد معين. ومن أمثلة الصوت النقي ذو تردد معين، التصفير بالفم أو دق أحد أوتار العود أو أحد أوتار البيانو أو القانون. كذلك تتصف الشوكة الرنانة بصوت له تردد معين (مثل 128/الثانية أو 512/الثانية وغيرها) يُستخدم لمعايرة الآلات الموسيقة.
وعندما يتكون الصوت الذي تسمعه الأذن من عدة ترددات (أي عدة من الموجات الجيبية) تلتقطه كضوضاء وشوشرة، وأحيانا تتداخل عدة ترددات صوتية وتستمتع الأذن بسماعها، ذلك لأن الموجات المتداخلة متوافقة، أي تتكون من موجة رئيسية مصحوبة بموجة أو موجات تنتمي إلى الموجة الرئيسية ولكنها أعلى منها في التردد.
انظر أيضًا
مراجع
- ^ "معلومات عن موجة جيبية على موقع jstor.org". jstor.org. مؤرشف من الأصل في 2020-05-11.
| موجة جيبية في المشاريع الشقيقة: | |