|
تضامنًا مع حق الشعب الفلسطيني |
معادلة تفاضلية
| معادلات تفاضلية |
|---|
 |
| نِطَاق |
| تصنيف |
| الحلول |
| أشخاص |
في الرياضيات، المعادلة التفاضلية هي معادلة تربط دالة واحدة أو أكثر ومشتقاتها.[1] في التطبيقات، تمثل الدوال عمومًا كميات مادية، وتمثل المشتقات معدلات التغيير الخاصة بها، وتعرف المعادلة التفاضلية العلاقة بين الاثنين.[2][3][4] نظرًا لأن هذه العلاقات شائعة جدًا، تلعب المعادلات التفاضلية دورًا بارزًا في العديد من التخصصات بما في ذلك الهندسة والفيزياء والاقتصاد وعلم الأحياء.
تتكون دراسة المعادلات التفاضلية بشكل أساسي من دراسة حلولها (مجموعة الوظائف التي تلبي المعادلة)، وخصائص حلولها. أبسط المعادلات التفاضلية يمكن حلها بواسطة صيغ واضحة. ومع ذلك، قد يتم تحديد العديد من خصائص حلول معادلة تفاضلية معينة دون حسابها بالضبط.
في حالة عدم توفر تعبير مغلق للحلول، قد يتم تقريب الحلول عدديًا باستخدام أجهزة الحاسوب. تركز نظرية الأنظمة الديناميكية على التحليل النوعي للأنظمة التي تصفها المعادلات التفاضلية، في حين تم تطوير العديد من الطرق العددية لتحديد الحلول مع درجة معينة من الدقة.
التاريخ
ظهرت المعادلات التفاضلية أولاً مع اختراع حساب التفاضل والتكامل من قبل نيوتن ولايبنز. في الفصل الثاني من عمله 1671، قام إسحاق نيوتن في كتابه طريقة التدفقات،[5] بإدراج ثلاثة أنواع من المعادلات التفاضلية:
وفي عام 1695 اقترح ياكوب بيرنولي معادلة بيرنولي التفاضلية.[6] معادلة تفاضلية عادية في شكلها التالي:
التي حاول لايبنز في العام التالي حلحلتها من خلال تبسيطها.[7]
تاريخيًا، درست معضلة اهتزاز حبل ما، حبل آلة موسيقية مثالاً، من طرف كل من لورن دالمبير وليونهارد أويلر ودانييل برنولي وجوزيف لوي لاغرانج.[4][8][9][10] وفي عام 1746، اكتشف لورن دالمبير معادلة الموجة أحادية البُعد وبعد عشر سنين، اكتشف أويلر معادلة الموجة ثلاثية الأبعاد.[11]
تم تطوير معادلة أويلر-لاغرانج في خمسينيات القرن الماضي من قبل أويلر ولاغرانج فيما يتعلق بدراساتهم لمشكلة التاوتكرون. هذه هي مشكلة تحديد منحنى تسقط عليه الجسيمات الموزونة إلى نقطة ثابتة في فترة زمنية محددة، بغض النظر عن نقطة البداية. قام لاغرانج بحل هذه المشكلة في عام 1755 وأرسل الحل إلى أويلر. قام كلاهما بتطوير طريقة لاجرانج وتطبيقها على الميكانيكا، مما أدى إلى صياغة ميكانيكا لاغرانج.
في عام 1822، نشر فورييه عمله حول تدفق الحرارة في كتابه النظرية التحليلية للحرارة،[12] حيث استند في تفكيره على قانون نيوتن للتبريد، أي أن تدفق الحرارة بين جزيئين متجاورين يتناسب مع اختلاف بسيط للغاية في درجات الحرارة. يحتوي هذا الكتاب على اقتراح فورييه لمعادلة الحرارة الخاصة به من أجل نشر الحرارة الموصلة. يتم الآن تدريس هذه المعادلة التفاضلية الجزئية لكل طالب في الفيزياء الرياضية.
مثال
في الفيزياء، المعادلة التفاضلية التي يحققها التوتر V بين مربطي المكثف اثناء الشحن (الدارة RC)
لدينا الحل العام يكتب على شكل:
تحديد الثابتين m وB
لدينا:
لنعوض في المعادلة التفاضلية:
الحل صالح مهما كان t وA يخالف 0
إذن: B-E=0
و 1-RCm=0. وبالتالي فإن B=Eوm=1/RC
إذن:
تحديد A حسب الشروط البدئية
عند t=0:
، إذن
طرق حل المعادلات التفاضلية
توجد طرق عديدة لحل المعادلات التفاضلية منها:
- بعض الطرق المستخدمة لحل المعادلات التفاضلية من الرتبة الأولى:
- فصل المتغيرات: وذلك بفصل المتغيرات x,dx في جهة وy,dy في جهة أخرى في جانبي المعادلة ومن ثم القيام بمكاملة الطرفين لتحصل على حل على شكل دالة عادية (y=f(x
- التعويض
- المعادلات الخطية
- برنولي
- بعض الطرق المستخدمة لحل المعادلات التفاضلية من الرتبة n:
- اختزال الرتبة
- تحديد المعاملات
- مبادلة المتغيرات
- طريقة كوشي-أويلر لحل المعادلات التي فيها رتبة المشتقة هو نفسه أس معاملها
- طريقة المتتابعات الأسية
ويوجد أكثر من أسلوب للحل العددي وكذلك التحليلي. كما توجد معادلات مشهورة مثل معادلات لابلاس وبرنولي وغيرهم.
درجة المعادلة التفاضلية
تتحدد درجة المعادلة التفاضلية حسب أس المشتق ذو الرتبة الأعلى. مثلا إذا كانت المعادلة التفاضلية من الرتبة الثالثة، أي أن أعلى تفاضل فيها هو التفاضل الثالث، فدرجة المعادلة تتحدد حسب أس هذا التفاضل، فإذا كان مرفوعا للأس 5 مثلا تكون المعادلة من الدرجة الخامسة، وهكذا دواليك.
أنواع المعادلات التفاضلية
العادية والجزئية
يمكن تقسيم المعادلات التفاضلية إلى قسمين :
- معادلات تفاضلية عادية تحتوي على توابع ذات متغير مستقل واحد ومشتقات هذا المتغير.
- معادلات تفاضلية جزئية تحتوي دوال رياضية لأكثر من متغير مستقل مع مشتقاتها الجزئية.
الخطية وغير الخطية
كل من المعادلات التفاضلية العادية والجزئية يمكن أن تصنف إلى خطية وغير خطية. وتكون المعادلة التفاضلية خطية بشرطين:
- إذا كانت معاملات المتغير التابع والمشتقات فيها دوال في المتغير المستقل فقط أو ثوابت.
- إذا كان المتغير التابع والمشتقات غير مرفوعة لأسس، أي أن كلها من الدرجة الأولى.
وتكون غير خطية فيما عدا ذلك.
كل معادلة تفاضلية خطية هي من الدرجة الأولى، بينما ليست كل المعادلات التفاضلية من الدرجة الأولى هي خطية، لأن الدرجة تتحدد حسب أس التفاضل الأعلى، ومن الممكن أن تكون التفاضلات الأقل مرفوعة لأسس غير الواحد دون أن يؤثر ذلك على الدرجة، وهذا يخل بشرط المعادلة الخطية.
معادلة برنولي التفاضلية من الرتبة الأولى والدرجة الأولى وليست معادلة خطية: n≠1
أمثلة
التطبيق
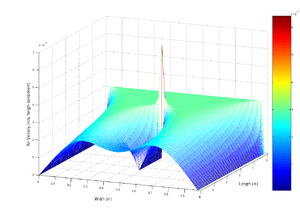
دراسة المعادلات التفاضلية هي مجال واسع في الرياضيات البحتة والتطبيقية والفيزياء والهندسة. جميع هذه التخصصات معنية بخصائص المعادلات التفاضلية بأنواعها المختلفة. تركز الرياضيات البحتة على وجود الحلول وتفردها، بينما تؤكد الرياضيات التطبيقية على التبرير الصارم لأساليب تقريب الحلول. تلعب المعادلات التفاضلية دورًا مهمًا في نمذجة كل عملية فيزيائية أو تقنية أو بيولوجية تقريبًا، بدءً من الحركة السماوية إلى تصميم الجسور وحتى التفاعلات بين الخلايا العصبية. قد لا تكون المعادلات التفاضلية مثل تلك المستخدمة في حل مشاكل الحياة الحقيقية بالضرورة قابلة للحل بشكل مباشر، على سبيل المثال لا يوجد لديها حلول شكل مغلقة. بدلاً من ذلك، يمكن تقريب الحلول باستخدام طرق عددية.
يمكن صياغة العديد من القوانين الأساسية للفيزياء والكيمياء كمعادلات تفاضلية. في علم الأحياء والاقتصاد، تستخدم المعادلات التفاضلية لنمذجة سلوك النظم المعقدة. تطورت النظرية الرياضية للمعادلات التفاضلية أولاً مع العلوم التي نشأت فيها المعادلات وحيث وجدت النتائج موضع التطبيق. ومع ذلك، فإن المشاكل المتنوعة، التي تنشأ في بعض الأحيان في مجالات علمية متميزة تمامًا، قد تؤدي إلى معادلات تفاضلية متطابقة. كلما حدث هذا، يمكن اعتبار النظرية الرياضية وراء المعادلات مبدأً موحداً وراء الظواهر المتنوعة. على سبيل المثال، فكر في انتشار الضوء والصوت في الجو، والأمواج على سطح البركة. يمكن وصفها جميعًا من خلال نفس المعادلة التفاضلية الجزئية من الدرجة الثانية، وهي معادلة الموجة، التي تسمح لنا بالتفكير في الضوء والصوت كأشكال من الأمواج، مثلها مثل الموجات المألوفة في الماء. يحكم توصيل الحرارة، التي طورها جوزيف فورييه، معادلة تفاضلية جزئية من الدرجة الثانية، معادلة الحرارة. اتضح أن العديد من عمليات الانتشار، رغم اختلافها على ما يبدو، يتم وصفها بنفس المعادلة؛ ترتبط معادلة بلاك-شولز في التمويل، على سبيل المثال، بمعادلة الحرارة.
انظر أيضًا
المراجع
- ^ Dennis G. Zill (15 مارس 2012). A First Course in Differential Equations with Modeling Applications. Cengage Learning. ISBN:1-285-40110-7. مؤرشف من الأصل في 2020-01-17.
- ^ Cannon، John T.؛ Dostrovsky، Sigalia (1981). "The evolution of dynamics, vibration theory from 1687 to 1742". Studies in the History of Mathematics and Physical Sciences. New York: Springer-Verlag. ج. 6: ix + 184 pp. ISBN:0-3879-0626-6.
{{استشهاد بدورية محكمة}}: الاستشهاد بدورية محكمة يطلب|دورية محكمة=(مساعدة)GRAY، JW (يوليو 1983). "BOOK REVIEWS" (PDF). Bulletin (New Series) of the American Mathematical Society. ج. 9 ع. 1. مؤرشف من الأصل (PDF) في 2016-12-29. اطلع عليه بتاريخ 2017-12-24.(retrieved 13 Nov 2012). - ^ GRAY، JW (يوليو 1983). "BOOK REVIEWS". Bulletin (New Series) of the American Mathematical Society. ج. 9 ع. 1.
- ^ أ ب Wheeler، Gerard F.؛ Crummett، William P. (1987). "The Vibrating String Controversy". Am. J. Phys. ج. 55 ع. 1: 33–37. Bibcode:1987AmJPh..55...33W. DOI:10.1119/1.15311.
- ^ Newton, Isaac. (c.1671). Methodus Fluxionum et Serierum Infinitarum (The Method of Fluxions and Infinite Series), published in 1736 [Opuscula, 1744, Vol. I. p. 66].
- ^ Bernoulli، Jacob (1695)، "Explicationes, Annotationes & Additiones ad ea, quae in Actis sup. de Curva Elastica, Isochrona Paracentrica, & Velaria, hinc inde memorata, & paratim controversa legundur; ubi de Linea mediarum directionum, alliisque novis"، Acta Eruditorum
- ^ Hairer، Ernst؛ Nørsett، Syvert Paul؛ Wanner، Gerhard (1993)، Solving ordinary differential equations I: Nonstiff problems، Berlin, New York: سبرنجر، ISBN:978-3-540-56670-0
- ^ Frasier، Craig (يوليو 1983). "Review of The evolution of dynamics, vibration theory from 1687 to 1742, by John T. Cannon and Sigalia Dostrovsky" (PDF). Bulletin (New Series) of the American Mathematical Society. ج. 9 ع. 1. مؤرشف من الأصل (PDF) في 2018-12-23.
- ^ For a special collection of the 9 groundbreaking papers by the three authors, see First Appearance of the wave equation: D'Alembert, Leonhard Euler, Daniel Bernoulli. - the controversy about vibrating strings (retrieved 13 Nov 2012). Herman HJ Lynge and Son. نسخة محفوظة 15 ديسمبر 2019 على موقع واي باك مشين.
- ^ For de Lagrange's contributions to the acoustic wave equation, can consult Acoustics: An Introduction to Its Physical Principles and Applications Allan D. Pierce, Acoustical Soc of America, 1989; page 18.(retrieved 9 Dec 2012) نسخة محفوظة 14 مارس 2017 على موقع واي باك مشين.
- ^ Speiser, David. Discovering the Principles of Mechanics 1600-1800, p. 191 (Basel: Birkhäuser, 2008). نسخة محفوظة 17 يناير 2020 على موقع واي باك مشين.
- ^ Fourier, Joseph (1822). Théorie analytique de la chaleur (بالفرنسية). Paris: Firmin Didot Père et Fils. OCLC:2688081. Archived from the original on 2020-04-08. Retrieved أغسطس 2020.
{{استشهاد بكتاب}}: تحقق من التاريخ في:|تاريخ الوصول=(help)
وصلات خارجية
| معادلة تفاضلية في المشاريع الشقيقة: | |